Mathematics is an incredible piece of abstract thinking through which humans have developed technology and a clearer understanding of nature. From counting stars in the sky to calculating quantum states of subatomic particles, Mathematics is a fundamental tool that we use to make sense of the world around us. Several species of animals can perform some type of mathematical calculations; like counting the number of animals in a rival group or dividing food fairly to nurture offspring. Given that Mathematics is not a way of thinking exclusive to humans, one can’t help but wonder at the logic behind it.
What is Mathematics?
Even though the definition of Mathematics is still up for debate, it is generally agreed upon that Mathematics has its foundations in logic. Logic, however, also lacks a clear definition but can be described as the reasoning behind certain rules and processes. The core of these rules is the validation of a given piece of information or the assessment of whether a statement is true or false. For example: “The earth is round” is a statement that can be assessed in terms of truthfulness. Using a primitive example, the statement “This is edible,” must be evaluated under the light of logic if a species is to survive. Under this perspective, the usefulness of logic in thinking is clear, because it helps living creatures understand and interact with the world around them.
Researchers have tried a wide range of experimental methods on different animal species in order to determine the extent to which animals apply logic to navigate situations. One of those trials involved a crow trying to figure out how to drink water from a narrow cylindrical glass that was half-filled. The picture below is that of the crow in action solving the problem. The crow successfully realized that the way to drink some water from the jar was to raise the level of water by dropping stones inside. This is proof that animals, to a large extent are capable of some sort of reasoning.

Through the process of natural selection, some species have evolved to use a more or less simplistic version of this survival skill, of assessing truthfulness in their environment to meet their needs. After millions of years, some creatures have developed more sophisticated brains than others, and this allows them to make more complex logical judgments. This implies better decisions. Humans are one of the most intelligent creatures on the planet thanks to these small but significant improvements in logical thinking which happened over time with the evolution process. Consequently, we have been able to adapt more to our environment. But how did logical thinking emerge in the first place? How can something so abstract be tackled by a bunch of neurons interacting?
Emergence Theory and The Development of Math
This phenomenon, in which a collection of simpler units (like a cell) gives rise to a more complex structure (like a brain) is called emergence. Emergence can be seen across all facets of nature. Water molecules in the air condense and form macroscopic structures (clouds) that travel through the air and can cause electrostatic effects in the atmosphere (lightning). An ant colony is made up of millions of ants that individually can’t understand the logistics of maintaining the colony, but can collectively adopt a system of keeping the colony safe, nurtured, and in constant growth (some even keep farms of fungi).
Also, consciousness itself; the phenomenon that allows you to be aware of your surroundings and your inner state, is something that emerges from patterns within the brain. All the above-mentioned occurrences in nature are examples of the theory of emergence at play. The leading theory on the emergence of complex thoughts in humans is similar to the emergence of consciousness, which is likely to have evolved from less complex lifeforms as a product of natural selection. It is in this way that Mathematics is theorized to have emerged from simple living units through the natural selection process.
Math, the Universe, and Everything
The wonderful thing about the tool of Mathematics is that it helps us construct big theories about the universe, and these theories actually work. An example is the invention of the GPS navigation system which was made possible by Einstein’s Theory of Relativity or Classical Mechanics. However, these theories are still incomplete, in the sense that they do not apply to every case we came across. For instance, ‘Classical Mechanics theory’ mostly only works with macroscopic objects (things we can see with the naked eye), but losing its veracity once studies move to sub-atomic scales.
To date, we have yet to derive a complete theory for all physical phenomenon, and achieving this would be difficult since our universe, despite obeying certain rules, has an infinite number of particles interacting, which makes it a complex system, to say the least. Even if we completely forget that the underlying nature of the universe is probabilistic (from Quantum Mechanics we know that the state of sub-atomic particles can be described by a wave function), non-probabilistic systems, like deterministic complex systems (our Universe in the macroscopic scale) can still give us a headache when trying to describe them with precision.
Fortunately, Mathematics is beginning to tackle these complex systems through a method called Chaos Theory. Complex systems are typically systems with a large number of particles that obey specific laws even while chaos emerges from these systems. Chaos arises whenever small disturbances in the system culminate to a big change at a later time; like the flap of the wings of a butterfly in Japan triggering a hurricane in the USA via the complex system of the atmosphere. Sounds incredible right?
The best-known example of a chaotic system is the Lorenz system, which serves as a model for structuring convection, the movement of air based on its temperature, in the atmosphere. The model is given by:
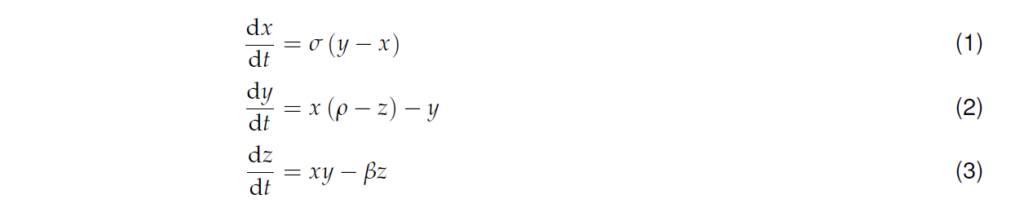
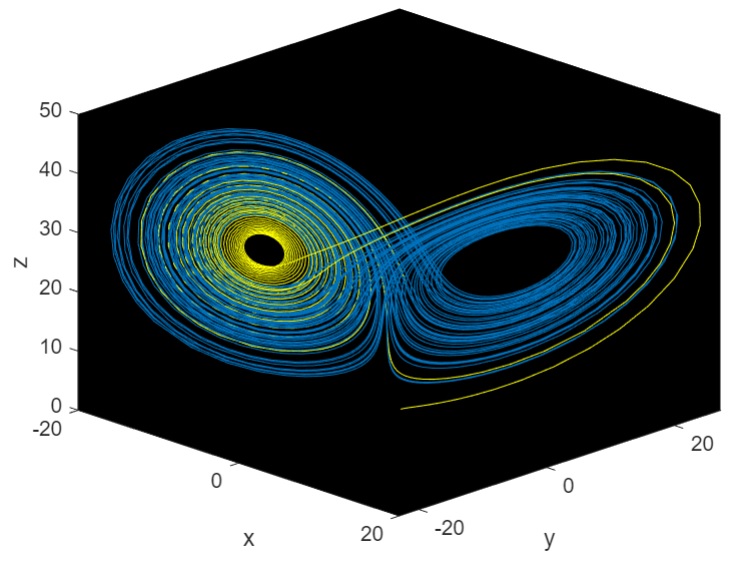
The diagram above illustrates the position of a particle moving along a chaotic solution for the Lorenz system. The initial position of the particle is on the graph at x, y, z = 1, 1, (the start of the yellow curve) and the solution is run for a total of 100-time units. The yellow curve represents the motion of the particle during the first 20 time units, changing to blue for the following time steps. The solution was derived using a numerical method called “Runge-Kutta” with MATLAB software.
The Lorenz attractor is a simple example of a physical system where the lack of perfect knowledge of the initial conditions compromises our ability to predict its future development. In a real-world scenario, we wouldn’t know for certain the initial position of the particle. This places emphasis on the fact that physical systems can be completely deterministic but still be inherently unpredictable even in the absence of quantum effects.
Despite all the complexity we see in our universe that makes unveiling the mysteries of reality a big challenge, the intrinsic way of reasoning we call Mathematics is sure to take us deep down the rabbit hole of knowledge. Also, what may even be more unpredictable than a complex system, is knowing just how far down the rabbit hole we will go.
Enjoyed this article? Visit the 4P Academy Blog for more informative pieces on a variety of fascinating topics.
SOURCES
Lorenz, E. N. Deterministic nonperiodic flow. In The Theory of Chaotic Attractors. Springer, New York, NY. 2004. (pp.25-36)
Lorenz, K. Das sogenannte :zur Naturgeschichte der Aggression. Wien : G. Borotha-Schoele . 1963. (Vol. 16).
Mueller, G. & Gerardo, N. Fungus-farming Insects: Multiple Origins and Diverse Evolutionary Histories. Proceedings of the National Academy of Sciences. 2002. 99(24), 15247-15249.
Tucker, W. The Lorenz attractor exists. Comptes Rendus de l’Académie des Sciences-Series I-Mathematics, 1999. 328(12), 1197-1202.
Turner, S. Crow Smarts: Inside the Brain of the World’s Brightest Bird. Houghton Mifflin Harcourt. 2016.