If you have watched Formula 1 racing or just racing in general, you would have noticed large wings on the backs of the cars. But have you ever wondered why they are there?
A Friction Problem
In most forms of racing the tracks are not straight; they have many twists and turns which the driver must navigate as fast as possible. To get around the corner quickly, the car has to grip well to the track, which means the tires have to create a force directed towards the center of the turn called centripetal force. The same concept is applied to race cars taking a corner at high speeds. Those of you familiar with friction would know that the force the tire can resist is proportional to the weight on the tire.
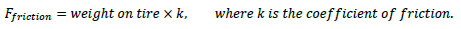
The more weight on the tire the harder it can grip. For a car to complete a turn successfully, the tire friction has to equal the centripetal force. Why not just add mass to the car then? Well, the centripetal force which the tire needs to keep the car on the ground is also proportional to the mass of the car.
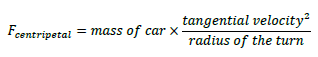
In other words, the heavier the car, the more centripetal force required. The tire would also need more frictional force to turn.
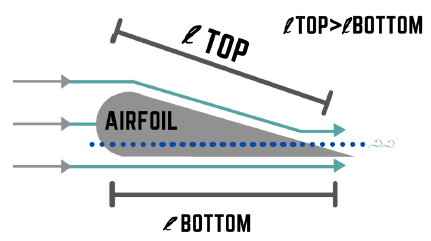
This small bit of math and physics hugely limits the speed at which a car can take turns, so racers and engineers were constantly trying to find a way to get around it. One day a Ferrari driver, Richie Ginther, saw that their cars were lifting at the rear and suggested the addition of a spoiler. The spoiler directed air slightly upwards and kept the rear end from lifting. It was the first use of a spoiler in racing. However, engineers later realized that the same airfoil shapes that allowed airplanes to fly could be inverted to produce negative lift, or a down force! The first use of a wing in Formula 1 racing was by the Lotus F1 team in 1967.
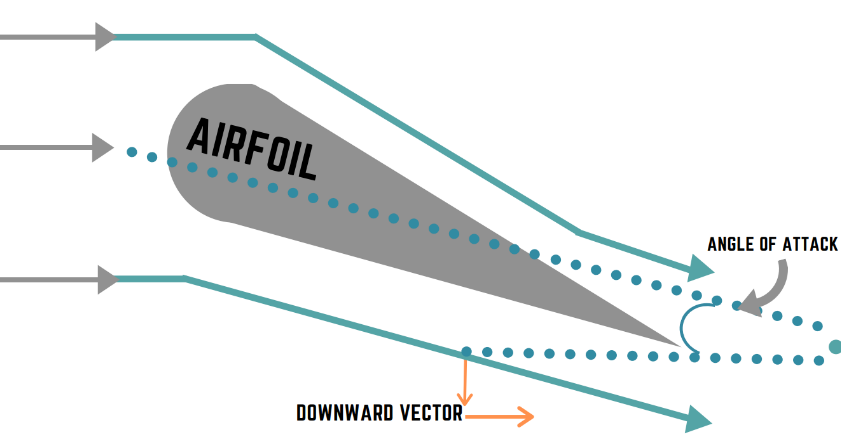
The airfoil shape is used by many flying objects from birds to airplanes and helicopters. In a typical airfoil, the path of air traveling over the top is longer than the path of air traveling under the wing. The air must meet at the end of the wing regardless of the distance it travels; thus the air traveling over the top has to move much more quickly to arrive at the same place as the air going underneath the foil. According to Bernoulli’s principle, the faster-moving air over the top has a lower pressure than the air traveling under the wing. The higher pressure underneath the wing then causes an upward force known as lift.
Bernoulli’s Principle
Bernoulli’s principle uses the Law of Conservation of Energy to describe the relationship between pressure, velocity, and potential energy. The Law of Conservation of Energy states that energy in a closed system cannot be created or destroyed; it can only be transformed into one form or another. In a substance such as air, energy can be transformed into pressure energy, kinetic energy, or potential energy.
Bernoulli’s equation is as follows:
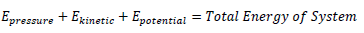
We are only interested in the difference in energy on the top of the wing and under the wing, so if the total energy of the system (the air flowing around the wing) is constant, we can write dual equations like this:

We can then equate both top and bottom equations since they both equal the total energy of the system.
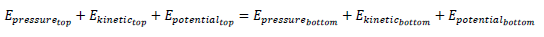
We normally see Bernoulli’s equation in a standard form like this:
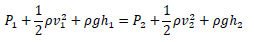
Where p, v, and ℎ are pressure, velocity, and height respectively. The subscript 1 and 2 can represent any two different positions; in our case top/bottom. In this idealized situation, we assume the air density to be constant. We can also use this equation in calculating the downforce generated by the rear diffuser, but that’s an article for another time.
Now, if we assume the difference between heights ℎ1 and ℎ2 are negligible and can therefore cancel each other out, which is true in the grand scheme of things because the thickness of wings is rather small relative to everything else in the car, we can write the equation as:
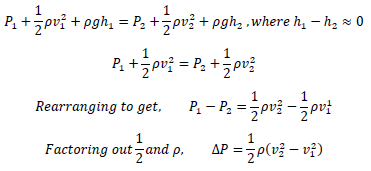
Voila! We get a simple equation to find out the difference in pressure on the top of the wing versus under the wing. Of course, this is a very basic equation for an ideal and unrealistic situation with many assumptions disregarding factors like turbulence and flow separation. However, if you are interested in fluid mechanics, there are plenty of resources and tutors at 4P Academy who would gladly help you explore this fascinating field.
Conservation of Momentum
There is another phenomenon at work as well. When wings are angled to direct air upwards or downwards, it also moves a mass of air up or down. With conservation of momentum or simply Newton’s third law, where, for every action, there is an opposite and equal reaction, moving air up or down results in a force on the wing in the opposite direction.

Wings on Race Cars

A combination of physics principles allows planes to fly and helps race cars stick to the ground; that is why we mount upside-down airfoils on race cars. The air flows around them and pushes them downwards, thereby adding weight to the wheels without increasing the centripetal force. Formula 1 cars are very lightweight and must rely on the massive downforce created by their airfoils, sometimes as much as three times the weight of the car, to turn corners very quickly.
However, one downside to using wings is the massive drag it produces. The larger the wing, or the steeper the wing angle, the greater the drag. Drag reduces the top speed of a car, which is why some racing series such as Formula 1 have a Drag Reduction System (DRS). It works by simply having a system to flatten the angle of the wing on straights or when overtaking, reducing drag and allowing higher speeds.
So, if you have ever wondered why F1 cars have wings, there goes your answer! Aerodynamics is just as important for cars as it is for airplanes. Most consumer vehicles have extensive aerodynamic considerations for stability and fuel economy reasons. I
f you are interested in topics like this, 4P Academy has plenty of knowledgeable tutors in these fields, who would gladly guide you through them.
Enjoyed this article? Visit the 4P Academy Blog for more informative pieces on a variety of fascinating topics.

